Inverse functions and differentiation

Short description: Calculus identity

Rule:
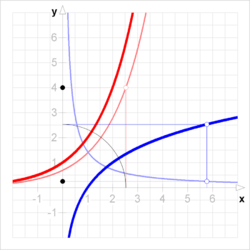
[math]\displaystyle{ {\color{CornflowerBlue}{f'}}(x) = \frac{1}{{\color{Salmon}{(f^{-1})'}}({\color{Blue}{f}}(x))} }[/math]

Example for arbitrary [math]\displaystyle{ x_0 \approx 5.8 }[/math]:
[math]\displaystyle{ {\color{CornflowerBlue}{f'}}(x_0) = \frac{1}{4} }[/math]
[math]\displaystyle{ {\color{Salmon}{(f^{-1})'}}({\color{Blue}{f}}(x_0)) = 4~ }[/math]

In mathematics, the inverse of a function [math]\displaystyle{ y = f(x) }[/math] is a function that, in some fashion, "undoes" the effect of [math]\displaystyle{ f }[/math] (see inverse function for a formal and detailed definition). The inverse of [math]\displaystyle{ f }[/math] is denoted as [math]\displaystyle{ f^{-1} }[/math], where [math]\displaystyle{ f^{-1}(y) = x }[/math] if and only if [math]\displaystyle{ f(x) = y }[/math].

Their two derivatives, assuming they exist, are reciprocal, as the Leibniz notation suggests; that is:

[math]\displaystyle{ \frac{dx}{dy}\,\cdot\, \frac{dy}{dx} = 1. }[/math]

This relation is obtained by differentiating the equation [math]\displaystyle{ f^{-1}(y)=x }[/math] in terms of x and applying the chain rule, yielding that:

[math]\displaystyle{ \frac{dx}{dy}\,\cdot\, \frac{dy}{dx} = \frac{dx}{dx} }[/math]

considering that the derivative of x with respect to x is 1.

Writing explicitly the dependence of y on x, and the point at which the differentiation takes place, the formula for the derivative of the inverse becomes (in Lagrange's notation):

[math]\displaystyle{ \left[f^{-1}\right]'(a)=\frac{1}{f'\left( f^{-1}(a) \right)} }[/math].

This formula holds in general whenever [math]\displaystyle{ f }[/math] is continuous and injective on an interval I, with [math]\displaystyle{ f }[/math] being differentiable at [math]\displaystyle{ f^{-1}(a) }[/math]([math]\displaystyle{ \in I }[/math]) and where[math]\displaystyle{ f'(f^{-1}(a)) \ne 0 }[/math]. The same formula is also equivalent to the expression

[math]\displaystyle{ \mathcal{D}\left[f^{-1}\right]=\frac{1}{(\mathcal{D} f)\circ \left(f^{-1}\right)}, }[/math]

where [math]\displaystyle{ \mathcal{D} }[/math] denotes the unary derivative operator (on the space of functions) and [math]\displaystyle{ \circ }[/math] denotes function composition.

Geometrically, a function and inverse function have graphs that are reflections, in the line [math]\displaystyle{ y=x }[/math]. This reflection operation turns the gradient of any line into its reciprocal.

Assuming that [math]\displaystyle{ f }[/math] has an inverse in a neighbourhood of [math]\displaystyle{ x }[/math] and that its derivative at that point is non-zero, its inverse is guaranteed to be differentiable at [math]\displaystyle{ x }[/math] and have a derivative given by the above formula.

Examples

• [math]\displaystyle{ y = x^2 }[/math] (for positive x) has inverse [math]\displaystyle{ x = \sqrt{y} }[/math].

[math]\displaystyle{ \frac{dy}{dx} = 2x \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \frac{dx}{dy} = \frac{1}{2\sqrt{y}}=\frac{1}{2x} }[/math]

[math]\displaystyle{ \frac{dy}{dx}\,\cdot\,\frac{dx}{dy} = 2x \cdot\frac{1}{2x} = 1. }[/math]

At [math]\displaystyle{ x=0 }[/math], however, there is a problem: the graph of the square root function becomes vertical, corresponding to a horizontal tangent for the square function.

• [math]\displaystyle{ y = e^x }[/math] (for real x) has inverse [math]\displaystyle{ x = \ln{y} }[/math] (for positive [math]\displaystyle{ y }[/math])

[math]\displaystyle{ \frac{dy}{dx} = e^x \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \frac{dx}{dy} = \frac{1}{y} }[/math]

[math]\displaystyle{ \frac{dy}{dx}\,\cdot\,\frac{dx}{dy} = e^x \cdot \frac{1}{y} = \frac{e^x}{e^x} = 1 }[/math]

Additional properties

• Integrating this relationship gives

[math]\displaystyle{ {f^{-1}}(x)=\int\frac{1}{f'({f^{-1}}(x))}\,{dx} + C. }[/math]

This is only useful if the integral exists. In particular we need [math]\displaystyle{ f'(x) }[/math] to be non-zero across the range of integration.

It follows that a function that has a continuous derivative has an inverse in a neighbourhood of every point where the derivative is non-zero. This need not be true if the derivative is not continuous.

• Another very interesting and useful property is the following:

[math]\displaystyle{ \int f^{-1}(x)\, {dx} = x f^{-1}(x) - F(f^{-1}(x)) + C }[/math]

Where [math]\displaystyle{ F }[/math] denotes the antiderivative of [math]\displaystyle{ f }[/math].

Higher derivatives

The chain rule given above is obtained by differentiating the identity [math]\displaystyle{ f^{-1}(f(x))=x }[/math] with respect to x. One can continue the same process for higher derivatives. Differentiating the identity twice with respect to x, one obtains

[math]\displaystyle{ \frac{d^2y}{dx^2}\,\cdot\,\frac{dx}{dy} + \frac{d}{dx} \left(\frac{dx}{dy}\right)\,\cdot\,\left(\frac{dy}{dx}\right) = 0, }[/math]

that is simplified further by the chain rule as

[math]\displaystyle{ \frac{d^2y}{dx^2}\,\cdot\,\frac{dx}{dy} + \frac{d^2x}{dy^2}\,\cdot\,\left(\frac{dy}{dx}\right)^2 = 0. }[/math]

Replacing the first derivative, using the identity obtained earlier, we get

[math]\displaystyle{ \frac{d^2y}{dx^2} = - \frac{d^2x}{dy^2}\,\cdot\,\left(\frac{dy}{dx}\right)^3. }[/math]

Similarly for the third derivative:

[math]\displaystyle{ \frac{d^3y}{dx^3} = - \frac{d^3x}{dy^3}\,\cdot\,\left(\frac{dy}{dx}\right)^4 - 3 \frac{d^2x}{dy^2}\,\cdot\,\frac{d^2y}{dx^2}\,\cdot\,\left(\frac{dy}{dx}\right)^2 }[/math]

or using the formula for the second derivative,

[math]\displaystyle{ \frac{d^3y}{dx^3} = - \frac{d^3x}{dy^3}\,\cdot\,\left(\frac{dy}{dx}\right)^4 + 3 \left(\frac{d^2x}{dy^2}\right)^2\,\cdot\,\left(\frac{dy}{dx}\right)^5 }[/math]

These formulas are generalized by the Faà di Bruno's formula.

These formulas can also be written using Lagrange's notation. If f and g are inverses, then

[math]\displaystyle{ g''(x) = \frac{-f''(g(x))}{[f'(g(x))]^3} }[/math]

Example

• [math]\displaystyle{ y = e^x }[/math] has the inverse [math]\displaystyle{ x = \ln y }[/math]. Using the formula for the second derivative of the inverse function,

[math]\displaystyle{ \frac{dy}{dx} = \frac{d^2y}{dx^2} = e^x = y \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \left(\frac{dy}{dx}\right)^3 = y^3; }[/math]

so that

[math]\displaystyle{ \frac{d^2x}{dy^2}\,\cdot\,y^3 + y = 0 \mbox{ }\mbox{ }\mbox{ }\mbox{ }; \mbox{ }\mbox{ }\mbox{ }\mbox{ } \frac{d^2x}{dy^2} = -\frac{1}{y^2} }[/math],

which agrees with the direct calculation.

See also

• Calculus
• Inverse functions
• Chain rule
• Inverse function theorem
• Implicit function theorem
• Integration of inverse functions